Эдгар По написал рассказ о дядьке, который случайно нашел зашифрованную записку, применил к ней в то время считавшиеся передовыми криптографические методы и в результате получил инструкцию по обретению пиратского клада. Сперва он произвел сложные логические ходы: определил, что послание написано на английском языке, и предположил, что каждая буква латинского алфавита везде заменена каким-то другим символом. Дальше чисто технические. Известно, что в любом языке одни буквы встречаются реже, а другие чаще. Исследовав достаточный массив текстов, можно определить, что это за буквы. Логично, что и в зашифрованном тексте символ, встречающийся наибольшее число раз, кодирует самую популярную букву, и так далее. Можно так расшифровать хотя бы часть текста, а дальше уже подбирать по смыслу.

Но это происходило в XIX веке, а сегодня криптографической деятельностью можно заниматься только специальным федеральным службам, поэтому простым любителям частотного анализа приходится искать другие области его применения. Например, капитал-шоу «Поле Чудес».

Типичная игра там проходит так: игроки видят, из скольких букв состоит слово; пытаются назвать буквы, которые вероятнее всего будут в этом слове (обычно гласные, они же во всех словах есть); затем, когда гласных набирается, на их взгляд, достаточно, пытаются угадать согласные, которые были бы уместны среди того, что уже получено; и наконец, когда открыто достаточно букв, чтобы исключить большинство вариантов, какой-то счастливчик называет слово. Таким образом, у каждого игрока в голове есть какая-то частотная модель русского языка, которой они пользуются, чтобы максимизировать вероятность угадывания. Причем эта модель должна отличаться от той, которой пользовался герой Эдгара По (и, как мне почему-то казалось, герой Артура Конана Дойля в «Пляшущих человечках», но там оказалась своя мистическая технология):

Во-первых, слова в игре выбираются случайно, в отличие от нашей речи, где одни есть чуть ли не в каждом предложении, а про другие никто никогда не слышал. Поэтому модель должна создаваться не по какому-то корпусу, а по словарю, учитывая каждое слово по одному разу.

Во-вторых, самые распространенные слова — в основном, предлоги, союзы и всё такое, — как и глаголы с именами прилагательными, вообще считать не надо, потому что в русских играх со словами (в отличие от английских, например) не принято их загадывать. Только нарицательные существительные.

В-третьих, не имеет значения, сколько раз встречается буква в слове. Игрок не целится в какую-то конкретную позицию, а говорит: «я думаю, что это слово, в котором присутствует буква Ю». И вероятность угадывания зависит уже от количества слов, в которых эта буква присутствует, а не от количества употреблений этой буквы.

Представьте, что вы оказались на телеигре, и попробуйте и у себя в голове построить такую модель. Какие буквы, на ваш взгляд, будут более популярными, а какие менее?

Я извлек из словаря Открытого корпуса русского языка все нарицательные существительные, которых вышло примерно 66 тысяч, обработал их и получил такой результат (буквы по убыванию частоты):

А О Е И Н Р Т К С Л В П Ь М Д У З Г Б Я Ц Ч Ф Ж Ш Х Ы Щ Й Э Ю Ъ

Немного отличается от обычной частотности (из Википедии на основе Национального корпуса русского языка):

О Е А И Н Т С Р В Л К М Д П У Я Ы Ь Г З Б Ч Й Х Ж Ш Ю Ц Щ Э Ф Ъ

Хотя и не очень.

В-четвертых, игрокам изначально известна длина слова. И это можно использовать, потому что в коротких словах чаще встречаются одни буквы, а в длинных другие.

Вот, например, по четырехбуквенным словам:

А Р О Е Т К Л С И У Н П Д М Б Г В З Ь Я Ш Ф Х Ч Ю Ж Й Э Ы Ц Щ Ъ

И по восьмибуквенным:

А О И Е Н Р К Т Л С П В М Д У Ь З Б Г Ч Я Ц Ш Ф Х Ж Й Ы Щ Э Ю Ъ

И в-пятых, в процессе игры ее участники получают новую информацию — о буквах, которых нет в слове, и о местонахождении тех, которые есть.

Учитывая эти пять пунктов, можно предложить такую стратегию: игрок, перед тем как назвать букву, выбирает из словаря все слова нужной длины, в которых не встречаются ошибочно названные буквы, а отгаданные стоят на соответствующих местах. Затем он подсчитывает для каждой буквы количество слов, в которых она встречается, и называет ту, для которой это число максимально. Мне кажется, любой участник «Поля чудес» способен проделать это, пока крутится барабан.

Недостатком этого алгоритма является то, что он детерминированный, то есть каждый раз можно предсказать, каким будет следующий ход. В теории игр существует понятие равновесия Нэша — состояния, когда всем участникам игры известны стратегии остальных, но ни один из них не может увеличить своего выигрыша, изменив свою стратегию, если у остальных участников она останется прежней. Если представить, что в «Поле чудес» есть два игрока, один из которых — Якубович, загадывающий слово, а другой — вся тройка, пытающаяся назвать как можно меньше букв, которых в слове нет, причем они побеждают, если отгадают слово, допустив менее какого-то фиксированного числа ошибок; так вот, если представить, то равновесия при использовании этой стратегии нет. Ведущий может подобрать слово, которое не получается отгадать, и каждый раз загадывать его. Немного (но далеко не полностью) приблизить равновесие Нэша можно, если делать выбор более случайно. Например, в какой-то момент посчитали, что буква А встречается в 5 словах, буква О — в 7, а буква Р — в 3. Тогда запускается генератор случайных чисел, с помощью которого с вероятностью 5/15 выбирается А, 7/15 — О и 3/15 — Р. В среднем это должно дать то же самое.

Чтобы выяснить, какие слова при такой игре окажутся самыми сложными, я промоделировал этот алгоритм на сингл-плеерном аналоге «Поля чудес» — «Виселице» (о которой, на самом деле, всё это время речь и шла). Поскольку никаких вычислительных ресурсов, кроме ноутбука, который можно оставить на ночь, у меня нет, то после нескольких часов с профилировщиком питона (благодаря которым я даже смог улучшить время работы в несколько раз!), было решено проводить исследования в три этапа:

1. Перебрать все 66 тысяч слов с помощью первого детерминированного варианта, чтобы отбросить наиболее легкие. Примерно в трети случаев слова были названы полностью без единой ошибки. В итоге, я оставил те десять тысяч, в которых отгадыватель предположил более трех букв неправильно.
2. Затем, прогнать каждое слово из оставшихся по 20 раз уже на случайном алгоритме. Тут появилась небольшая проблема с тем, что требовалось определиться, сколько ошибок можно сделать до того, как игрока повесят. Просто отгадывать до конца, а потом посчитать среднее, нельзя: поражение с пороговым числом ошибок и поражение с числом, превышающим его, по сути одинаковы. Оказалось, что единого мнения о количестве деталей на рисунке с висельником, нет. Пришлось прикинуть: столб, перекладина, петля, голова, туловище, правая рука, левая рука, правая нога, левая нога, посиневший язык. Итого десять.
3. Около четырехсот слов, которые не были отгаданы более, чем в половине случаев, я прогнал уже немного более масштабно: по 100 раз каждое. Топ по числу поражений выглядит так:

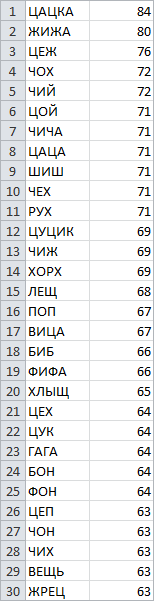
Такие результаты объяснимы (кроме слова цой, которое внезапно оказалось нарицательным, но составители словаря наверняка знали, что делали). Самыми сложными оказались не длинные непонятные слова — в таких встречается много разных букв, поэтому вероятность ошибки мала, — а короткие с редкими и иногда с повторяющимися буквами, чтобы попасть в правильную было как можно труднее. В случае с цацкой не помогает даже легко отгадываемая буква А: в словаре было двести пятибуквенных слов с А на второй и последней позициях.

А перед тем, как начнется рекламная пауза, я хочу передать привет Саше, Саше, Антону, Сереже, Насте, Саше, Оле, Толику, Юле, Анюте, Богдану и всем остальным, кто может меня читать.